Arduino.ru

Пару лет назад, я написал пост, но, как выяснил только сегодня, забыл его выложить :(

А сегодня так получилось, что о нём вспомнил, меня попросили ссылку, а ссылки-то и нету – не нашёл. Зато нашёл «черновики», потому выкладываю сейчас.

(формулы и доказательства, выведенные карандашом на бумаге, я не буду вдаваться в подробности вывода и доказательства, чтобы не перегружать материал)

Итак, всем известно (а кому неизвестно – знайте), что millis() принимает не все значения с шагом 1. Некоторые пропускает. Убедиться в этом легко, запустить вот такой скетч:

void setup(void) {
	Serial.begin(57600);
}

void loop(void) {
	static uint32_t oldMillis = 0;
	const uint32_t currentMillis = millis();
	if (currentMillis == oldMillis) return; // значение не успело поменяться
	if (currentMillis - oldMillis > 1) { // Если пропущено значение
		Serial.println(oldMillis + 1); // Печатаем пропущенное значение
	}
	oldMillis = currentMillis;
}

его результат в мониторе порта:

42
85
127
170
213
255
298
341
383
426
469
511
554
.....

все эти числа millis() пропустила. Т.е. была равна, например, 84, и сразу скакнула на 86.

Меня заинтересовало, можно ли получить полный список таких «ненавидимых миллисом» чисел.

Посмотрел на текст millis(). Если немного упростить (убрать заморочки про атомарность), то выглядит он вот так:

uint32_t gCounter = 0;
uint32_t timer0_overflow_count = 0;
uint32_t timer0_millis = 0;
uint8_t timer0_fract = 0;

#define F_CPU	16000000LL
#define MICROSECONDS_PER_TIMER0_OVERFLOW 1000000LL*64*256/F_CPU		// 1024
#define MILLIS_INC (MICROSECONDS_PER_TIMER0_OVERFLOW / 1000)		// 1
#define FRACT_INC ((MICROSECONDS_PER_TIMER0_OVERFLOW % 1000) >> 3)	// 3
#define FRACT_MAX (1000 >> 3)										// 125

inline void overflowHandler(void) {
	uint32_t m = timer0_millis;
	unsigned char f = timer0_fract;
	m += MILLIS_INC;
	f += FRACT_INC;
	if (f >= FRACT_MAX) {
		f -= FRACT_MAX;
		m += 1;
	}
	timer0_fract = f;
	timer0_millis = m;
	timer0_overflow_count++;
}

inline uint32_t millis(void) { return timer0_millis; }

Ну, собственно, причина пропускания понятна - прерывание происходит не через 1000 микросекунд, а через 1024. Погрешность по-возможности компенсируется, но иногда для такой компенсации требуется пропустить значения.

Повозившись пару часов с карандашом в руке, я таки вывел общую формулу, позволяющую выловить все такие числа до единого. Формула получилась рекуррентная, правда, но всё же. Вот она: millis() пропускает значения следующей последовательности S:

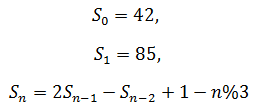
где n > 1, а знак % обозначает операцию взятия остатка от деления.

Теперь можно сказать, что мы знаем все числа, которые пропускает millis. Всего таких чисел 100 663 296.

Поигравшись со всем этим ещё немного, я заметил интересую закономерность, которую после некоторых усилий сумел даже доказать, а именно - сюда попадают все числа вида 2ⁿ-1 при n от семи до 32. Т.е. миллис никогда не вернёт значения 0xFFFFFFFF или там 0x0000FFFF. Не знаю, как для кого, но для меня это было неожиданно и забавно.

Ну, и, наконец, я решил таки проверить, а не ошибся ли я в каких-то выкладках и решил тупо в лоб всё просчитать (прямо до 2³²), чтобы быть полностью уверенным, что мои замечательные результаты не являются следствие случайной потери знака или ещё какой описки. Для этого написал программу (на для Ардуино - та больно долго бы считала - на своём ноутбуке запускал). Программ делает следующее:

1) эмулирует алгоритм millis() и сравнивает пропущенные числа с полученными по формуле
2) подсчитывает общее количество таких пропущенных чисел
3) проверяет действительно ли все до единого числа вида 2ⁿ-1 при n от семи до 32 пропускаются.

Вот текст:

#include "pch.h"
#include <iostream>
#include <time.h>

//
//	Все числа вида 2^(n-1) для 7 <= n <= 32
//
const uint32_t specialNumbers[] = {
	0x0000007F, 0x000000FF, 0x000001FF, 0x000003FF, 0x000007FF, 0x00000FFF,
	0x00001FFF, 0x00003FFF, 0x00007FFF, 0x0000FFFF, 0x0001FFFF, 0x0003FFFF,
	0x0007FFFF, 0x000FFFFF, 0x001FFFFF, 0x003FFFFF, 0x007FFFFF, 0x00FFFFFF,
	0x01FFFFFF, 0x03FFFFFF, 0x07FFFFFF, 0x0FFFFFFF, 0x1FFFFFFF, 0x3FFFFFFF,
	0x7FFFFFFF, 0xFFFFFFFF
};

uint32_t gCounter = 0;
uint32_t timer0_overflow_count = 0;
uint32_t timer0_millis = 0;
uint8_t timer0_fract = 0;

/////////////////////////////////////
//
//	В точности повторяем расчёт millis из wiring.c
//
#define F_CPU	16000000LL
#define MICROSECONDS_PER_TIMER0_OVERFLOW 1000000LL*64*256/F_CPU		// 1024
#define MILLIS_INC (MICROSECONDS_PER_TIMER0_OVERFLOW / 1000)		// 1
#define FRACT_INC ((MICROSECONDS_PER_TIMER0_OVERFLOW % 1000) >> 3)	// 3
#define FRACT_MAX (1000 >> 3)										// 125

inline void overflowHandler(void) {
	uint32_t m = timer0_millis;
	unsigned char f = timer0_fract;
	m += MILLIS_INC;
	f += FRACT_INC;
	if (f >= FRACT_MAX) {
		f -= FRACT_MAX;
		m += 1;
	}
	timer0_fract = f;
	timer0_millis = m;
	timer0_overflow_count++;
}

inline uint32_t millis(void) { return timer0_millis; }

/////////////////////////////////////
//
//	Реализация реккурентной формулы
//		m0=42, m1=85, mN = 2*(mN-1) - (mN-2) + 1 - N%3 
//
inline uint32_t getNum(void) {
	static uint32_t m1, m2;
	if (gCounter == 0) {
		gCounter++;
		return m2 = 42;
	}
	if (gCounter == 1) {
		gCounter++;
		return m1 = 85;
	}
	const uint32_t res = 2 * m1 - m2 + 1 - (uint8_t)(gCounter % 3);
	m2 = m1;
	m1 = res;
	gCounter++;
	return res;
}

////////////////////////////////////////////
//
//	Собственно, всё веселье здесь.
//
int main(void) {
	const time_t start = time(NULL);
	for (bool continueFlag = true; continueFlag; ) {
		const uint32_t oldM = millis();
		overflowHandler();
		const uint32_t diff = millis() - oldM;
		if (diff != 1) { // Если число пропущено
			// Берём очередное число по формуле и сравниваем с пропущенным
			const uint32_t num = getNum();
			if (num != oldM + 1) {	// Если не совпало, выдаём сообщение
				std::cout << "*** " << gCounter << ": " << (oldM + 1) << "" << num << std::endl;
				exit(0);
			}
			static int sCnt = 0;
			if (specialNumbers[sCnt] == num) {
				printf("Got 0x%08X\n", num);
				sCnt++;
			}
			continueFlag = ! (gCounter > 1 && num == 42);
			//
			// Если хочется посмотреть на пропущенные числа, можно 
			// раскомментировать, но считаться будет долго!
			//std::cout << gCounter << "\t" << num << std::endl;
		}
	} 
	const double diff = difftime(time(NULL), start);
	std::cout << "Total: " << (gCounter - 1) << "; time: " << diff << " seconds." << std::endl;
}

Вот результат работы:

Got 0x0000007F
Got 0x000000FF
Got 0x000001FF
Got 0x000003FF
Got 0x000007FF
Got 0x00000FFF
Got 0x00001FFF
Got 0x00003FFF
Got 0x00007FFF
Got 0x0000FFFF
Got 0x0001FFFF
Got 0x0003FFFF
Got 0x0007FFFF
Got 0x000FFFFF
Got 0x001FFFFF
Got 0x003FFFFF
Got 0x007FFFFF
Got 0x00FFFFFF
Got 0x01FFFFFF
Got 0x03FFFFFF
Got 0x07FFFFFF
Got 0x0FFFFFFF
Got 0x1FFFFFFF
Got 0x3FFFFFFF
Got 0x7FFFFFFF
Got 0xFFFFFFFF
Total: 100663296; time: 27 seconds.

Как видите, всё подтвердилось.

Не знаю какова практическая польза от того, что мы теперь знаем какие числа не нравятся millis(), по мне так никакой, но повозиться было забавно.

Удачи всем!