Arduino.ru

Для чего я это здесь размещаю? Хрен его знает, наверное на тот случай, если кто-то из студентов, например, ищет тему для научной работы или просто найдётся энтузиаст, который захочет подумать не просто о «движении робота по линии», но и об оптимальности его манёвров. Ну, и наконец, кому-то может быть просто любопытно узнать новое, безо всяких последующих действий. В общем, если кто-то заинтересуется - буду рад, если же нет - никто (кроме моих пальцев) не пострадает.

Для начала небольшое пояснение «на пальцах».

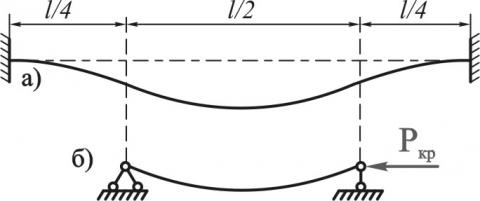
Предположим, что у Вас есть прямой упругий, гибкий стержень, концы которого закреплены на свободных шарнирах. Мы начинаем сдавливать этот стержень вдоль его оси. При некотором усилии стержень «выгнется» и будет выглядеть примерно так, как показано на рисунке (б) ниже. А если концы стержня жёстко закреплены? Он всё равно выгнется, но выглядеть будет уже так, как показано на рисунке (а).

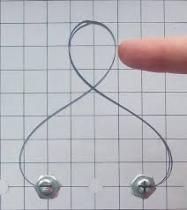
Ну а если мы закрепим концы и начнём сдавливать не вдоль оси, а «вертеть как попало»? Изгиб стержня в этом случае может принимать самые разные формы, например:

Причём формы эти устойчивы. Если приложить дополнительное усилие и деформировать стержень (палец на картинках), после того, как усилие будет снято, он восстановит свою форму. Значит есть что-то в этих кривых «оптимальное» - просто так ведь ничего не бывает, правда?

Всевозможные кривые, которые получаются при изгибу упругого гибкого стержня называются «эластиками Эйлера». Существует их полная классификация и вообще много там уже наворочено.

Оказывается, что эти самые эластики обладают целым рядом замечательных свойств. Например, это оптимальная (по затратам на маневрирование и удержание транспортного средства на траектории) траектория прохождения поворота. Если идти строго по эластике, то можно пройти поворот на максимально возможной скорости. И там много-много чего ещё (например, восстановление частично стёртых изображений и т.д.).

Более того, представьте тележку с двухколёсным прицепом, крепящемся в одной точке. Угадайте по какой кривой будут двигаться колёса прицепа при манёврах тележки? А какова оптимальная траектория прохождения поворота таким «автопоездом»? Правильно - тележка - по эластике, а прицеп - по своей эластике, через излом.

Ну, хватит, общего введения, переходим к Ардуиновским делам.

Есть знакомая команда математиков, которые исследуют эластики на предмет создания роботизированных решений для автотранспорта (в т.ч. автопоездов), стыковочных алгоритмов космических и подводных аппаратов и тому подобных задач. А для создания прототипов и экспериментов с ними они использую Ардуино (и как догадались?).

Вот полюбуйтесь на одну из их статей. Там подробно описывается маленький Ардуино-робот, который шастает вдоль эйлеровских эластик. Проблемы с роботом, которые у них возникли, всем знакомы - аж родным чем-то пахнуло.

Буду рад, если кому-то было интересно, даже не в плане самому заняться, а просто прочитать.